Chapter 3
SRUTIS AND THEIR FUNDAMENTAL PROPERTIES
3.4.1 The cycle of fifths and the cycle of fourths
One way of deriving the 22 srutis of our music is to use the well-known cycle of fourths and the cycle of fifths. The ‘fifth’ note referred to above is nothing but panchama and the ‘fourth note’ is the swara suddha madhyama.
In the cycle of fifths, we first consider the note panchama whose relative frequency is 3/2. Now the panchama of this panchama has the relative frequency of (3/2) x (3/2) which is equal to 9/4. This number may be identified as the relative frequency of the note chatusruti rishabha in the tara sthayi. Again, considering the panchama of this note we get the number (9/4) x (3/2) which is equal to 27/8. This number may be identified as the relative frequency of chatusruti dhaivata of tara sthayi. In this way one can build a series of numbers. Whenever the number exceeds 2, we divide it by 2 (or a suitable power of 2) so that the resultant number is always less than 2 and hence represents a sruti in the Madhya sthayi. The sequence of numbers so obtained constitutes the srutis of the cycle of fifths. Note that the sruti of suddha madhyama does not appear in this cycle.
The srutis belonging to the cycle of fifths may also be derived easily using the cents scale. The starting note is the panchama whose relative frequency is 702 cents. The next note in the sequence is the panchama of this panchama, which is obtained by simply adding 702 to this, which gives 1404 cents. The procedure may be repeated by successive addition of 702 cents to the numbers previously obtained. Whenever the number exceeds 1200 cents it is brought back to the Madhya sthayi by subtracting 1200 (or a suitable multiple of this). The cycle of fifths is shown in Table 3.3. In this table, the cycle of fifths is shown up to the 22nd cycle. Note that this cycle can be continued indefinitely.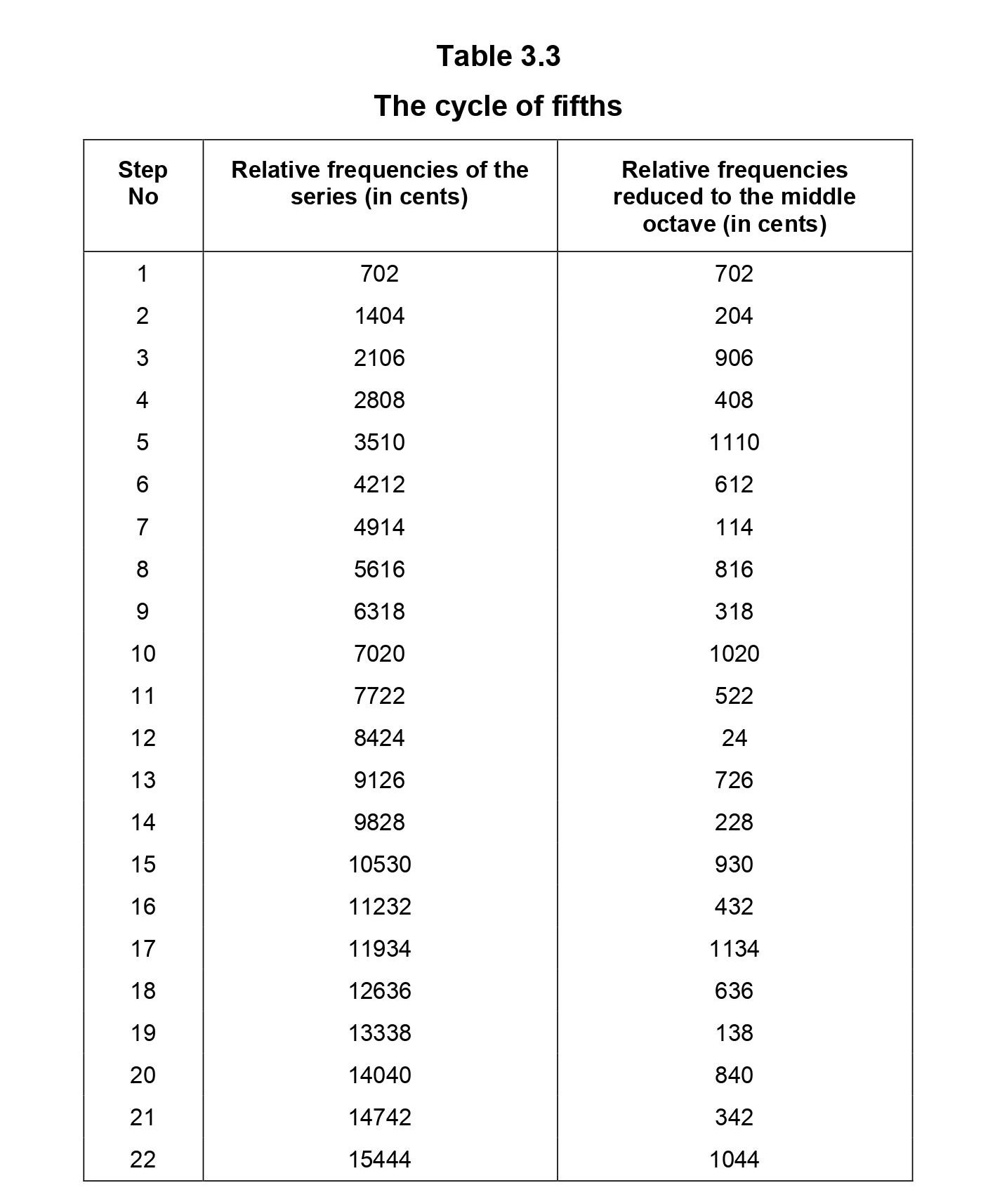
The process of the cycle of fourths is analogous to the cycle of fifths except that the note suddha madhyama is used in place of panchama. Again we first consider the note suddha madhyama whose relative frequency is 4/3. Now the suddha madhyama of this suddha madhyama has the relative frequency of (4/3) x (4/3) which is equal to 16/9. This number may be identified as the relative frequency of the note kaishiki nishada. Again considering the suddha madhyama of this note we get the number (16/9) x (4/3) which is equal to 64/27. This number may be identified as the relative frequency of sadharana gandhara of tara sthayi. In this way one can build a series of numbers. Whenever the number exceeds 2, we divide it by 2 (or a suitable power of 2) so that the resultant number is always less than 2 and hence represents a sruti in the Madhya sthayi.
The sequence of numbers so obtained constitutes the srutis of the cycle of fourths. Note that the sruti of panchama does the appear in this cycle. The
srutis belonging to the cycle of fourths may also be derived easily using the cents scale. The starting note is the note suddha madhyama whose relative frequency is 498 cents. The next note in the sequence is the suddha madhyama of this suddha madhyama, which is obtained by simply adding 498 to this which gives 996 cents. The procedure may be repeated by successive addition of 498 cents to the numbers previously obtained. Whenever the number exceeds 1200 cents it is brought back to the Madhya sthayi by subtracting 1200 (or a suitable multiple of this). The cycle of fourths is shown in Table 3.4. In this table also, the cycle of fourths is shown up to the 22nd cycle. Note that this cycle can be continued indefinitely.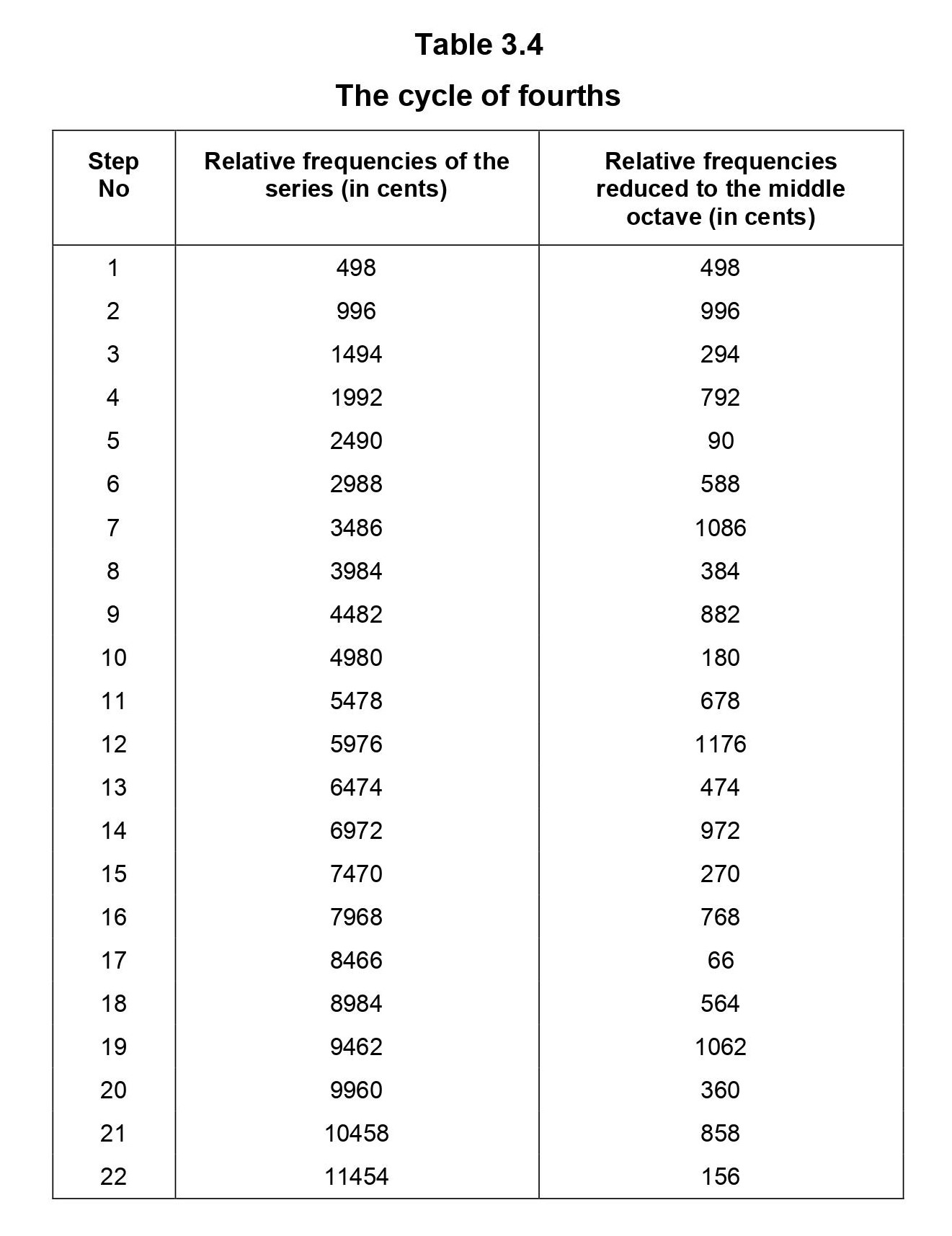
3.4.2 Choosing the 22 srutis
It may be seen now from Table 3.3 that at the 12th stage, the resultant frequency in the cycle of fifths comes close to the adhara shadja ( 0 cents) differing from it only by 24 cents corresponding to a ratio of 1.01396:1. This suggests that the process has completed one full circle, coming back to the adhara shadja once again. Hence all frequencies appearing in the sequence beyond and including the 12th stage are neglected and only the first 11 srutis in the cycle of fifths are selected. Similarly, in the cycle of fourths the resultant frequency at the 12th stage comes close to the tara sthayi shadja ( 1200 cents) differing from it only by 24 cents, thus completing one full circle. Hence all frequencies appearing in the sequence beyond and including the 12th stage are neglected and only the first 11 srutis in the cycle of fourths are selected. Together, these two make up for the 22 srutis of our musical scale. The 22 srutis are shown in Table 3.5. To avoid conflict with the notation used earlier, lower case letters are used to denote the 22 srutis other than shadja and anchama. The table lists these srutis and shows the relative frequencies in 3 formats—in cents, as actual numbers, and as ratios. It is, however, convenient to work with cents because these are handy numbers. This table also gives the difference between consecutive srutis in cents.
One of the serious drawbacks in the above method based on the cycles of fourths and fifths is that there is no strict rationale for the determination of the 22 srutis. These srutis are merely selected from the endless list of srutis formed by the cycle of fourths and the cycle of fifths. (The set of first 11 frequencies each from the cycle of fifths and the cycle of fourths.) The cycles of fifths and the fourths do not reveal why the 22 srutis are formed the way they are. Another drawback is that even though the numerical values of the srutis are known they do not reveal which exact swara they correspond to.
Earlier in this chapter, the relative frequencies of each of the dominant swaras were derived from first principles. Using this as the base, the system of 22 srutis is also derived from first principles. The derivation presented in section 3.4.4 tells us why there are only 22 srutis in this system. Before going into this section, we will take a close look at the properties of these 22 srutis.
3.4.3 Properties of the 22 srutis
It may now be observed from the last column of Table 3.5 that there are three differential values amongst the srutis. The lowest one is 24 cents, which has been referred to as the pramana sruti, in our musical literature. This is commonly called as a comma. The next one is 66 cents and is the nyuna sruti, while the third is 90 cents, called poorna sruti.
A remarkable property of these srutis is that they occur as closely located pairs, the difference between them being a pramana sruti. (See Fig.3.1b.) Thus, suddha rishabha, denoted as r1 has its twin note r2 which is located a pramana sruti higher. Chatusruti rishabha r4 has its twin note r3 located a pramana sruti lower and so on. Even panchama has a twin note,
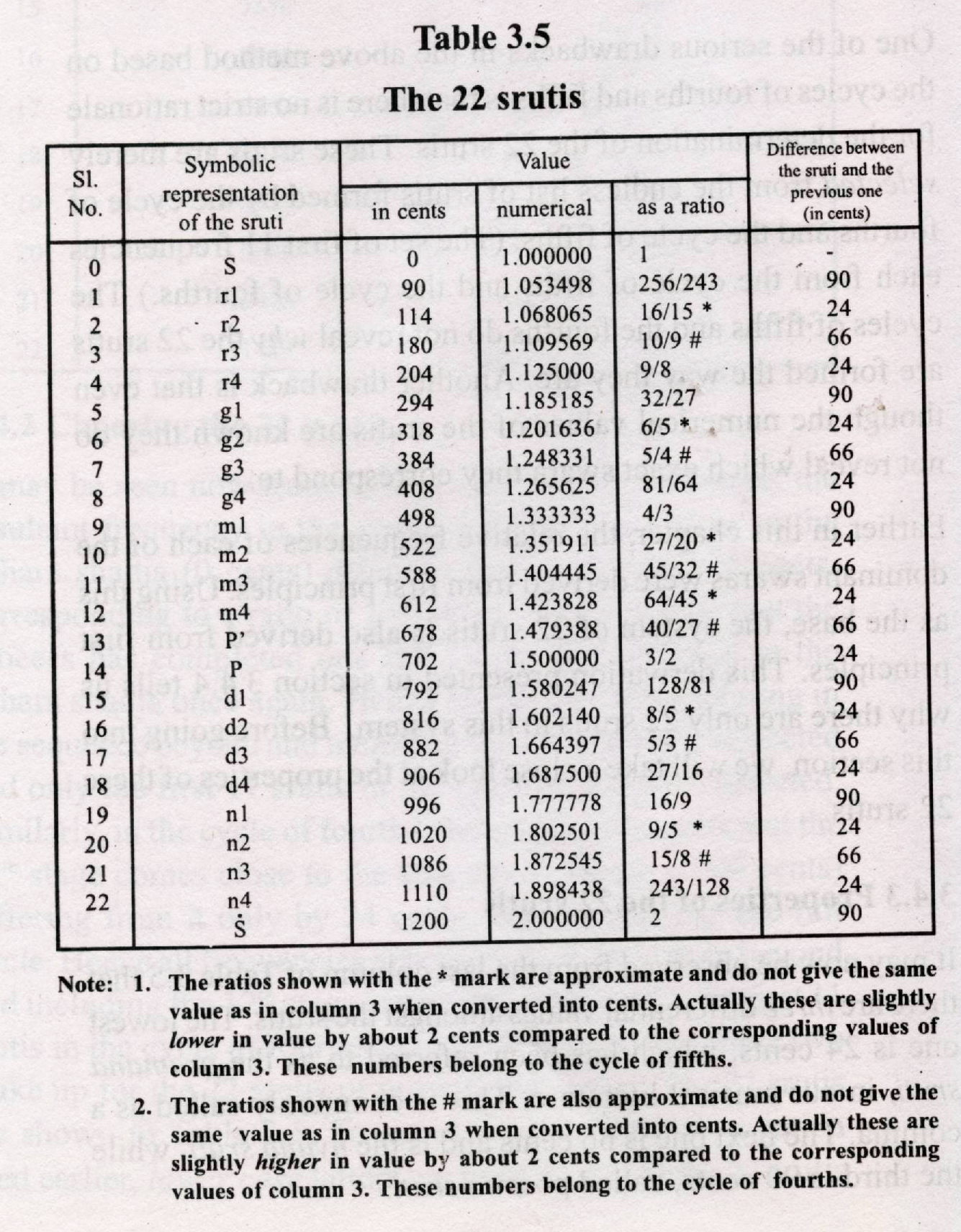
the displaced panchama, located a pramana sruti below it. One can thus see 11 pairs of srutis, of which the notes of the lower pitch belong to the cycle of fourths and the notes of the higher pitch belong to the cycle of fifths. Thus each of the 12 dominant notes has a twin counterpart belonging to the systems of 22 srutis. With this arrangement we now have four swarasthanas each for the five notes rishabha, madhyama, dhaivata, nishada, and two swarasthanas for the note panchama, thus constituting the 22 srutis. Note that in this reckoning of the 22 srutis, the adhara shadja is not included.
– to be continued
