Chapter – 3 (continued)
SRUTIS AND THEIR FUNDAMENTAL PROPERTIES
3.4.4 Analytical derivation of the 22 srutis
We begin by referring to Table 3.2. which summarizes the relative frequencies of the 12 dominant swaras. This table is seen slightly modified in Table 3.6 to show the values in cents. It may be seen from the above table, that the 12 swaras of our scale are unequally spaced. The difference between consecutive notes is either 256/243 (90 cents) or 2187/2048 (114 cents). (In the tempered scale of Western music, every note in the scale is spaced equally with a difference of exactly 100 cents.) The difference between these two is a comma, with a value equal to 24 cents.
Let us now consider what happens when modal shift of tonic is applied to ragas. Consider, for example, raga Kanakangi whose swaras are :
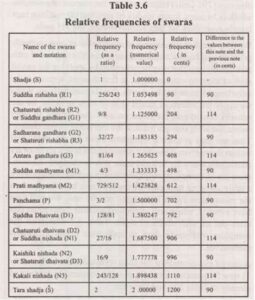
Swaras S R1 G1 M1 P D1 N1 Ṡ Ṙ1
Relative frequency 0 90 204 498 702 792 906 1200 1290 In cents
0 114 408 612 702 816 1110 1200
Consider now the rishabha moorchana. The new swaras under this moorchana are obtained by subtracting the values shown above in cents by that of the rishabha which is 90 cents. The resulting frequencies are:
In the above, the relative frequencies 408 6 1 2 702.1110 and 1200 may be identified as the swaras antara gandhara, prati madhyama, panchama, kakali nishada and tara sthayi shadja respectively. The relative frequencies that are shown underlined differ from the ideal values shown in the above table and are actually two new frequencies. These two frequencies differ from the ideal values of suddha rishabha (90 cents) and suddha dhaiyata (792 cents) repectively by the amount of a comma, which is 24 cents. It may readily be seen that the resulting raga largely resembles the raga Kamavardhini, the 51st mela.
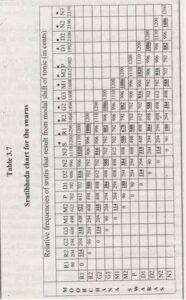
We now see that the process of modal shift of tonic actually generates additional frequencies or srutis. The number of such additional srutis that may be generated by applying the modal shift of tonic to various ragas, at first thought, appears to be quite large. But, as will be shown, this is not actually so. When we apply srutibheda or modal shift of tonic to ragas, we are actually considering the effect on individual swaras. In other words, the scale changes because the individual swaras change. Thus we may prepare it srutibheda chart for the individual swaras themselves. This chart demonstrates how a given swara transforms when the original tonic note is changed. As seen, there are 11 swaras excluding the shadja and we could prepare a table showing how each of these swaras transforms when the moorchana swara is changed one by one. We will thus have a matrix, which will include all possible frequencies that arise out of such shifts of tonic. Table 3.7 illustrates the complete srutibheda chart as applicable to the 11 swaras themselves.
A careful examination of this chart reveals that there are exactly 11 new frequencies ( in addition to the frequencies considered already in Table 3.6) and these are :
114, 180, 318, 384, 522, 588, 678, 816, 882, 1020 and 1086.
Note that many of the numbers appear repeatedly in Table
3.7. However, in Table 3.7 there is absolutely no other frequency except those listed above and the original 11 srutis.
Thus we have conclusively established from first principles that there are in all 11+11 = 22 srutis within an octave. Note that in this reckoning, the adhara shadja is not actually included.
Our ancient musicologists always interpreted sruti as an interval and it is thus logical to omit the trivial frequency of adhara shadja, which, by definition, is 0 cent.
- Comparison of the frequencies computed above with
those derived from the cycle of fifths and the cycle of fourths
In Tables 3.3 and 3.4 the cycles are shown up to the 22nd cycle. Now consider these two cycles up to the 11th step. It may be observed that the 22 srutis that are computed in Table 3.7
match perfectly with those computed from the cycles of fifths and fourths.
- Correspondence between the srutis obtained from the cycles of fifths and fourths and those obtained from the method of modal shift of tonic
It may be seen from the above that the frequencies computed from the method of modal shift of tonic as applied to individual swaras match perfectly with those computed from the cycles of fifths and fourths (put together). This suggests that there must be a close similarity between these two processes.
To validate this point, we again apply the modal shift of tonic now to all the 22 srutis computed previously. The process is same as that employed at the beginning for the 12 swaras. This process again generates 22 new srutis whose relative frequencies ( in cents
) are arranged in an ascending order in the following. (As this chart is very cumbersome with 22 x 22 entries, it is not shown here):
24, 66, 138, 156, 228, 270, 342, 360, 432, 474, 564, 636, 726,
768, 840, 858, 930, 972, 1044, 1062, 1134 and 1176.
It may now be observed that these are the very same frequencies that appear in the cycles of fifths and fourths as seen from the entries from the 12th cycle to 22nd cycle of Tables 3.3 and 3.4 (put together).
Thus the set of frequencies generated by the cycles of fifths and fourths is the same as that obtained from successive application of modal shift of tonic to the set of swaras, starting initially with the 12 swaras.
Thus, in the first instance, we have the 12 swaras or 11 srutis. By applying modal shift of tonic to this set, we obtain additional 11 srutis, totaling to 22 srutis. Again by applying modal shift of tonic to these 22 srutis, we get additional 22 srutis, totaling 44 srutis. As seen, all these sets of swaras match perfectly with the corresponding sets of swaras computed from the cycles of fifths and fourths put together.
The set of 44 srutis described above is only of academic interest, and it was derived merely to establish the one-to-one correspondence between the method of modal shift of tonic and the cyclic process of fifths and fourths. In fact this process may be repeated to get sequences of 88.176…..srutis and so on. As mentioned, only the sequence of 22 srutis is of importance as these are immediately linked to the 12 basic swaras of our scale.
We thus see that the set of 22 srutis belongs to a logical set of srutis. Of these, 11 srutis are those of dominant swaras listed in Table 3.2 and the other 11 srutis originate because of the difference in the sruti intervals between the dominant notes.
- Errors in the depiction of the 22 srutis in the earlier work
Sambamurthy has described the 22 srutis in considerable detail. (See for example his book South Indian Music, Vol.V, Chapters I and II.) However, there are certain errors in his description of these 22 srutis and they have been pointed out here. For easy comparison, Sambamurthy’s description of the 22 srutis and their correct description are illustrated in a pictorial form in the same figure (3.1a & 3.1b).
The following observations are now in order.
- The sruti P’ with a relative frequency 678 cents has been omitted by This frequency comes both in the cycle of the fourths. (see Table 3.4) and also in the present approach (see Table 3.7, 8th row, 15th column). Also Sambamurthy reckons the adhara shadja as one of the srutis to adjust for the loss of count of this sruti. This is clearly incorrect since the sruti has always been defined as an interval by ancient musicologists. According to the definition then, there will be only 21 srutis within an octave. On the other hand, inclusion of this sruti P’ (of 678 cents) in the list gives exactly 22 srutis with in an octave. This sruti is lower than panchama by a pramana sruti. Note the lack of symmetry in Fig.3.1a due to the omission of this sruti.
- As seen from Table 3.5, the correct value of the pramana sruti is 24 cents and that of the nyuna sruti 66 The values given by Sambamurthy for these two srutis are 22 and 70 cents respectively. Thus his value of the pramana sruti has an error of 2 cents and that of the nyuna sruti, 4 cents.
- In column 5 of Table 3.5 the list of the ratios which approximate the true values of the srutis is In fact, this is an excellent approximation differing from the true values (shown in cents in column 3 of the same table) only by +2 cents. These ratios are the ones adopted as the standard srutis by the Music Academy, Madras in 1929, excepting the displaced panchama P’. Logically however the correct values are those in column 3 (cents) or column 4 (numerical value) of Table 3.5 and not those ratios. Sambamurthy used these approximate ratios as reference values and suggested that those derived from the cycles of fourths and fifths need to be corrected by + 2 cents as applicable ( See page 43, Vol V of his book South Indian Music) As already seen, the values derived from the cycles of fourths and fifths are the correct ones as confirmed by the analysis presented here. Hence no adjustments in the srutis are necessary.
– to be continued…..



